Binäre Suchbäume vs Binärbäume

1. Begründen Sie bei welchem der folgenden Bäume es sich nicht um einen binären Suchbaum handelt

a)

           22
       /       \
     15         33
    /  \      /  |  \
  -4    5    32  33  34

33a = 33, musste es so schreiben, da 33 schon benutzt wird

graph TD;
    22 --> 15;
    22 --> 33;
    15 --> -4;
    15 --> 5;
    33 --> 32;
    33 --> 33a;
    33 --> 34;

Kein Binärer Suchbaum, da 33 mehr als 2 Kinder hat
Normalerweise ist in einem Binären Suchbaum keine Duplikate erlaubt, da gilt :
- Alle Werte im linken Teilbaum eines Knotens müssen kleiner als der Wert des Knotens selbst sein
- Alle Werte im rechten Teilbaum eines Knotens müssen größer als der Wert des Knotens selbst sein
- (es gibt Ausnahmen aber diese sind dann, extra definiert. In der Schule eigentlich nie definiert ausser dein Lehrer sagt was anderes)

b)

Binärer Suchbaum
- Jeder Knoten $\leq$ 2 Kinder
- Linker Teilbaum immer kleiner als Knoten
- Rechter Teilbaum immer größer als Knoten

c)

       26.03.2001
       /          \
  05.06.2000     02.10.2001
       \            /
    24.12.2000  05.10.2001

Der gegebene Baum ist kein binärer Suchbaum (BST), da die Eigenschaft verletzt wird, dass alle Knoten im linken Teilbaum kleiner und alle Knoten im rechten Teilbaum größer als der aktuelle Knoten sein müssen. Der Knoten 05.10.2001 im linken Teilbaum von 02.10.2001 ist jedoch größer, was gegen die BST-Regeln verstößt.

Annahme: Die Datumsangaben im Baum werden chronologisch geordnet, wobei frühere Daten als “kleiner” und spätere Daten als “größer” betrachtet werden. Diese Annahme basiert auf dem zeitlichen Ablauf der Daten und dient als Vergleichslogik für die Behandlung des Baumes als BST.

d)

implementieren
      \
   implodieren
         \
     imponieren
           \
     imprägnieren
               \
       improvisieren

implementieren und implodieren

1	2	3	4	5	6	7	8	9	10	11	12	13
i	m	p	l	e	m	e	n	t	i	e	r	e
i	m	p	l	o	d	i	e	r	e	n

Unterscheiden sich erst im 5. Character e vs o
"o" > "e" => true
implodieren steht richtigerweise rechts von implementieren

implodieren und imponieren

Position	1	2	3	4	5	6	7	8	9	10	11
implodieren	i	m	p	l	o	d	i	e	r	e	n
imponieren	i	m	p	o	n	i	e	r	e	n

Unterscheiden sich erst im 4. Zeichen: l vs o
Vergleich: 'o' > 'l' ist true (da der Unicode-Wert von ‘o’ (111) größer ist als der von ‘l’ (108))
Folgerung: imponieren steht richtigerweise rechts von implodieren

imponieren und imprägnieren

Position	1	2	3	4	5	6	7	8	9	10	11	12
imponieren	i	m	p	o	n	i	e	r	e	n
imprägnieren	i	m	p	r	ä	g	n	i	e	r	e	n

Unterscheiden sich erst im 4. Zeichen: o vs r
Vergleich: 'r' > 'o' ist true (Unicode-Wert von ‘r’ (114) > ‘o’ (111))
Folgerung: imprägnieren steht richtigerweise rechts von imponieren

imprägnieren und improvisieren

Position	1	2	3	4	5	6	7	8	9	10	11	12	13
imprägnieren	i	m	p	r	ä	g	n	i	e	r	e	n
improvisieren	i	m	p	r	o	v	i	s	i	e	r	e	n

Unterscheiden sich erst im 5. Zeichen: ä vs o
Vergleich:
- Unicode-Wert von 'ä' (228) und 'o' (111)
- 'ä' < 'o' ist false
Folgerung: improvisieren steht FÄLSCHLICHERWEISE rechts von imprägnieren

Zusammenfassung des Baums

Der resultierende richtige binäre Suchbaum basierend auf den Vergleichen sieht wie folgt aus:

        implementieren
               \
           implodieren
                  \
              imponieren
                    \
                imprägnieren
                  /
          improvisieren

Anmerkung: improvisieren ist ein linker Kindknoten von imprägnieren, da 'o' < 'ä'.

Erklärung der Vergleiche

Bei der Erstellung des Baums werden die Wörter nach lexikografischer Ordnung sortiert, basierend auf dem Vergleich der einzelnen Zeichen (Unicode-Werte):

Vergleich von Zeichen an gleicher Position: Beginne beim ersten Zeichen und vergleiche jedes Zeichen der Wörter nacheinander.
Entscheidungspunkt: Sobald ein Unterschied festgestellt wird, entscheidet der Vergleich der Unicode-Werte, in welche Richtung der Baum verzweigt.
- Wenn das Zeichen des neuen Wortes größer ist, geht es nach rechts.
- Wenn es kleiner ist, geht es nach links.
Fortsetzung des Prozesses: Wiederhole den Vergleich an der Position des Unterschieds für die weiteren Wörter, um ihre Position im Baum zu bestimmen.

Fazit

Der gegebene Baum ist kein Binärer Suchbaum

2. Ordnen Sie jede der gegebenen Darstellungen begründet einer oder mehrerer der folgenden Strukturen zu:

a)

Wahrscheinlichkeitsbaum (Entscheidungsbaum).
Keine Werte in der Wurzel → kein Binärbaum oder binärer Suchbaum.
Knoten repräsentieren Wahrscheinlichkeiten, nicht sortierte Werte.
Kein typischer Baum, da die Wurzel leer ist.

b)

Binärbaum, da jeder Knoten maximal zwei Kinder hat.
Kein binärer Suchbaum, da die Knoten nicht nach einer bestimmten Regel (z.B. Zahlenordnung) sortiert sind.

c)

Kein Baum, da zyklische Verbindung zwischen Frankfurt,Würzburg und Köln
- impliziert auch eine Verbindung auf gleicher Ebene (Frankfurt und Würzburg), was nicht erlaubt ist

d)

Baum, aber kein Binärbaum, da Schule mehr als 2 Kinder hat.
Somit auch kein Binärbaum
→ Directory Tree / Ordnerbaum / Verzeichnisbaum

Aufgabe 3

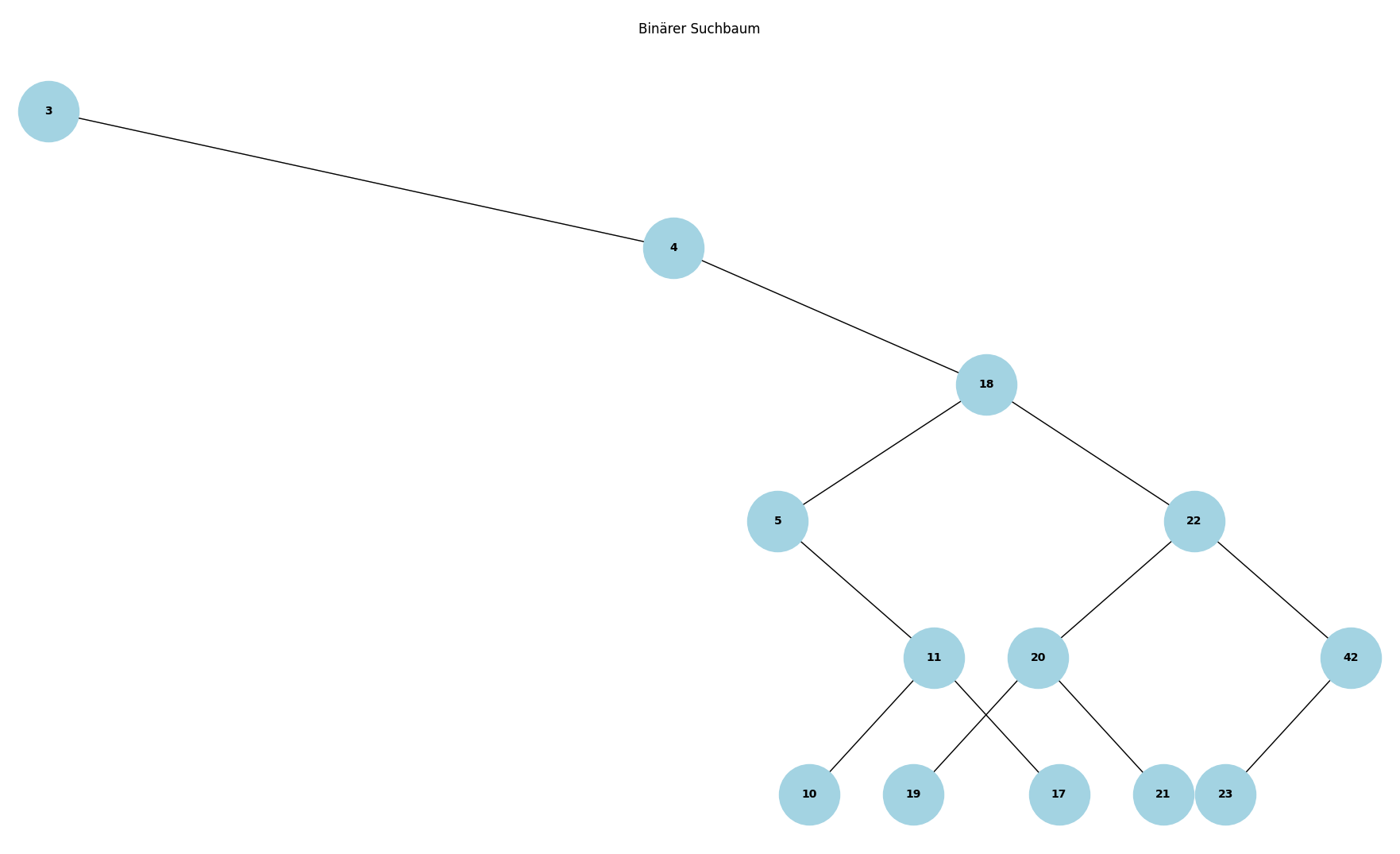
a) Geben Sie den binären Suchbaum an, der entsteht, wenn nacheinander die untenstehenden Schlüssel eingefügt werden.

17; 23; 42; 19; 10; 11; 5; 21; 20; 22; 18; 4; 3

Geben Sie den Baum an, der entsteht, wenn anschließend die Knoten mit den Schlüsseln 5 und 23 aus dem Suchbaum entfernt werden.

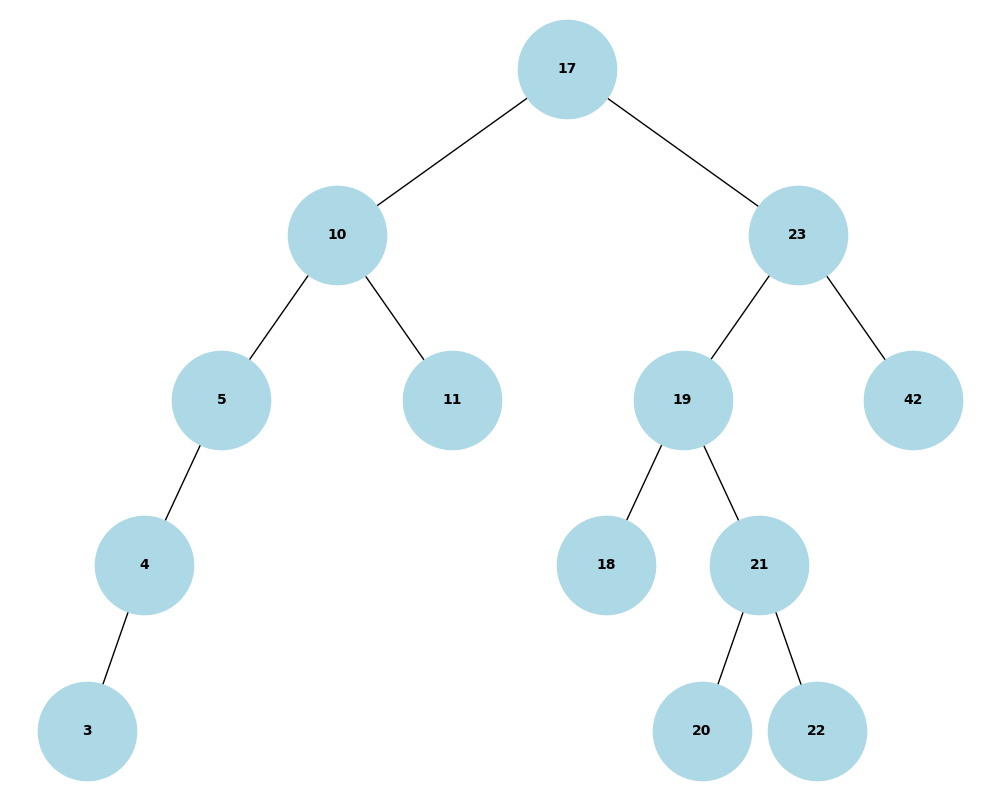
Baum nach dem Entfernen von 5 und 23:

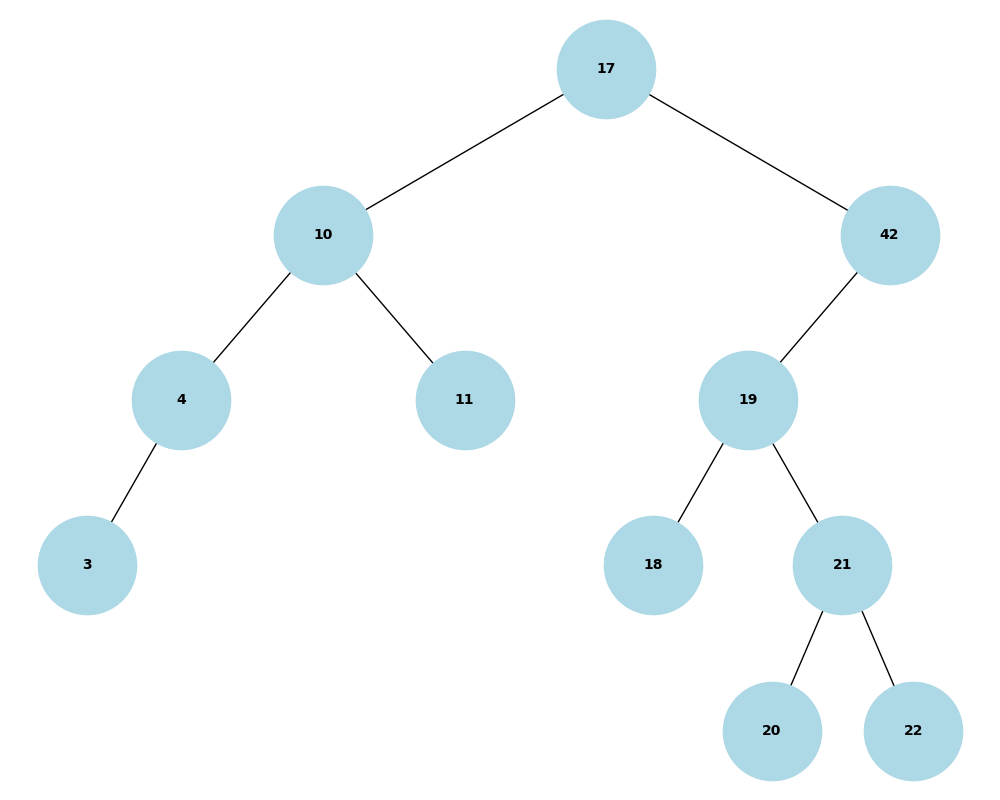
Um die Knoten mit den Schlüsseln 5 und 23 aus dem binären Suchbaum zu entfernen, müssen wir eine Funktion implementieren, die diese Schlüssel korrekt aus dem Baum löscht. Dabei gibt es drei Fälle, die beim Entfernen eines Knotens zu berücksichtigen sind:

Der Knoten hat keine Kinder (Blattknoten): Der Knoten wird einfach gelöscht.
Der Knoten hat ein Kind: Der Knoten wird gelöscht, und sein Kind ersetzt ihn.
Der Knoten hat zwei Kinder: Der Knoten wird durch den Nachfolger im Inorder-Traversal (den kleinsten Knoten im rechten Teilbaum) ersetzt.

Weiters Beispiel

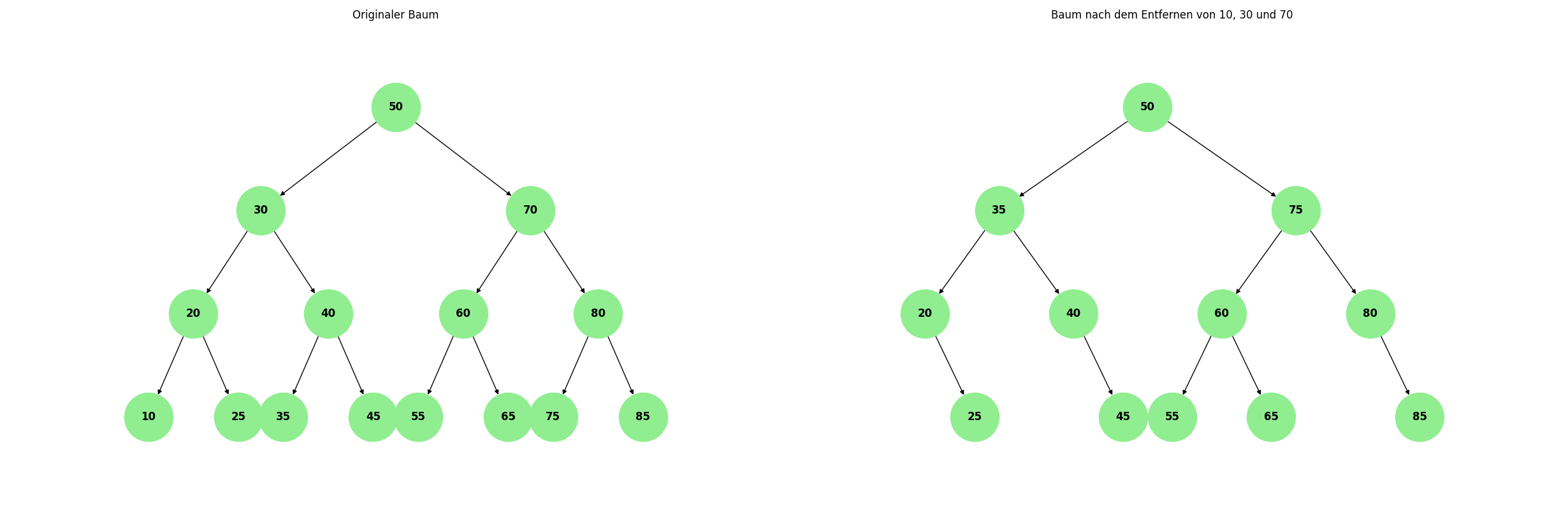
b) Geben Sie den binären Suchbaum an, der entsteht, wenn die obigen Schlüssel in umgekehrter Reihenfolge eingefügt werden.

3, 4, 18, 22, 20, 21, 5, 11, 10, 19, 42, 23, 17

c) Die Preorder-Ausgabe eines Suchbaums lautet: 12, 3, 0, 2, 7, 14, 13, 18, 15, 21. Zeichnen Sie den zugehörigen Suchbaum.

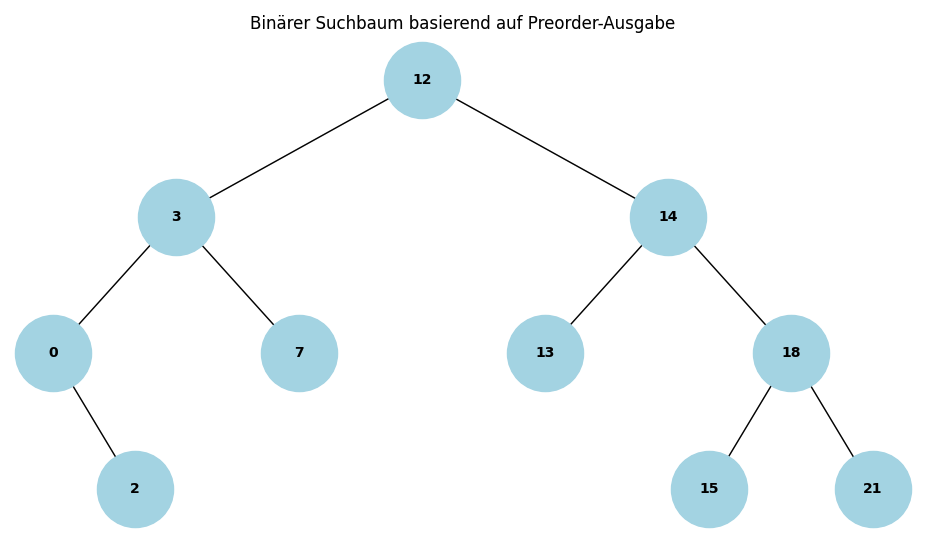
d) Entwickeln Sie eine Strategie, um das größte Element in einem binären Suchbaum aufzufinden.

public static  void maxElement(Node n) {  
    if (n == null) {  
        return;  
    }  
    while (n.right != null) n = n.right;  
    System.out.println("\n"+"Max Element: "+n.value);  
}

🎓 MyUniNotes - Nachhilfe

Explorer

(Übung)-5.3 Nicht-lineare Datenstrukturen